Detecção de onsets
Sumário
Apesar de a detecção de onset ser um assunto bem maduro na comunidade de Recuperação de Informação Musical, encontrei muito pouco material em português e, por isso, decidi unir o útil ao agradável e fazer esse textinho aqui, comentando um pouco do que tenho estudado. Junto com o texto, pretendo disponibilizar as poucas implementações que tenho feito e alguns experimentos.
Se você veio parar por aqui por acaso, fique à vontade e espero que aproveite a viagem.
Vamo que vamo!
Introdução
Um onset é o nome que é dado ao início de uma nota. Existem algumas discussões sobre onde de fato uma nota é iniciada, ainda mais por envolver questões como a nossa percepção. Por isso, o onset pode ter três definições diferentes:
- NOT (Note Onset Time): seria o momento exato em que a nota é iniciada. Isso se torna mais simples de entender quando temos, por exemplo, um áudio MIDI em que você especifica o momento no tempo em que a nota deve acontecer.
- AOT (Acoustic Onset Time): esse seria o momento em que a nota é mensurável. Ou seja, marcamos a sua posição no momento em que a identificamos e conseguimos medir.
- POT (Perceptual Onset Time): esse tipo de marcação considera o momento em que uma nota consegue ser percebida pelo ser humano.
A detecção de onsets não é uma tarefa nova na área, contudo ela é a base para várias outras tarefas que ainda estão sendo discutidas, pesquisadas e exploradas, como detecção de tempo e análise de ritmo, ainda mais se considerarmos os gêneros musicais que não estão no mainstream, como músicas tradicionais de diversos países que são muito pouco exploradas nas pesquisas da área.
Ouça o áudio abaixo. É bem fácil indicar cada uma das notas sem nem olhar para a frequência do sinal, né? Mas quantas músicas você conhece que tem apenas um instrumento?
Agora vamos para um áudio com mais instrumentos. O que você acha da forma de onda? Será que é possível olhar apenas para a amplitude e dizer onde cada nota começa?
Um último exemplo completamente caótico:
Quanto mais complexo o som, mais difícil é acertamos o início de cada nota para cada instrumento que é adicionado. Por isso diferentes métodos analisam vários atributos do nosso sinal de áudio, como a energia, a frequência e a fase.
Função novidade
Bom, dada essa grande introdução, agora vamos pra parte um pouco mais focada. A gente precisa arranjar um jeito de detectar eventos novos no nosso sinal e pra isso vamos precisar manipular o conteúdo do nosso sinal. É aqui que entra a função novidade.
Função novidade é um nome bonito e genérico para a seréie de transformações que vamos aplicar no nosso sinal para que tenhamos no fim uma representação de potenciais onsets. Note que a função novidade não é o último passo ainda de todo o nosso processamento: nesse passo, vamos identificar diferentes eventos que ocorrem, mas isso não significa que esses eventos sejam onsets. Diferentes eventos podem parecer com onsets, como vibratos ou mesmo ruídos externos, mas nós iremos filtrar.
Função novidade baseada em energia
O modo mais simples de se perceber quando há um onset ou um evento de algum instrumento no sinal musical é olhando apenas para a energia desse sinal. Intuitivamente, sabemos que se uma nota foi tocada a energia do sinal deve sofrer um aumento, já que estamos adicionando algo. Da mesma forma, quando essa nota acabar, o sinal retorna ao seu estado original.
A energia do sinal é dada pelo cálculo da amplitude do sinal ao quadrado ($x^2$) e queremos esse valor para cada uma das janelas (frames) do nosso áudio, portanto temos
\[E_w^x(n) = \left|\sum_{m \in \mathbb{Z}} x(m)w(m-n)\right|^2\]A aplicação da janela nada mais é do que a filtragem do sinal e por isso essa operação é feita por meio de uma convolução circular.
Ainda falando sobre a janela: neste caso, usamos a janela de Hann, que busca suavizar alguns efeitos de borda. Se não tivéssemos definido nenhuma janela e só selecionado um trecho do sinal, estaríamos aplicando uma janela retangular, que vale 1 para o intervalo que está definida e 0 para o resto.
Uma vez que temos a energia local do sinal, precisamos determinar quando um evento de fato aconteceu e, para isso, usamos a diferenciação (a famosa derivada!). No caso de um sinal discreto como o nosso, podemos fazer isso ao subtrairmos o sinal de sua versão deslocada em uma amostra, tal que
\[E_w^x(n+1) - E_w^x(n)\]Calculada a diferença, temos que notar que o resultado ainda não reflete os eventos de início de nota que queremos, mas sim todos os eventos. Para isso, aplicamos um retificador de meia onda. A operação é bem mais simples que o nome e consiste em removermos as partes negativas do nosso sinal resultante, para que possamos analisar apenas os eventos que vêm de diferenças positivas, ou seja, de aumentos de energia.
Em resumo, temos
\[\Delta_{Energia} = \left|E_w^x(n+1) - E_w^x(n)\right|_{\geq 0}\]Calcular a função novidade dessa forma faz com que onsets fracos sejam ignorados e, uma das abordagens pra corrigir isso é aplicar o logaritmo no sinal e fazer o cálculo. Isso pode fazer com que alguns ruídos também sejam amplificados.
\[\Delta_{Log Energia} = \left|\log{(E_w^x(n+1))} - \log{(E_w^x(n))}\right|_{\geq 0} = \left|\log{\left(\frac{E_w^x(n+1)}{E_w^x(n)}\right)}\right|_{\geq 0}\]Aplicando essa função ao nosso sinal do trompete, podemos ver que as marcações de onset, mesmo sem aplicarmos a detecção de picos, estão bastante alinhadas com os inícios das notas tocadas. Isso é porque, no geral, a função novidade baseada em energia funciona bem em sinais monofônicos. Uma rápida observação: o sinal da música foi normalizado para que ficasse mais simples de visualizar onde os onsets foram apontados.
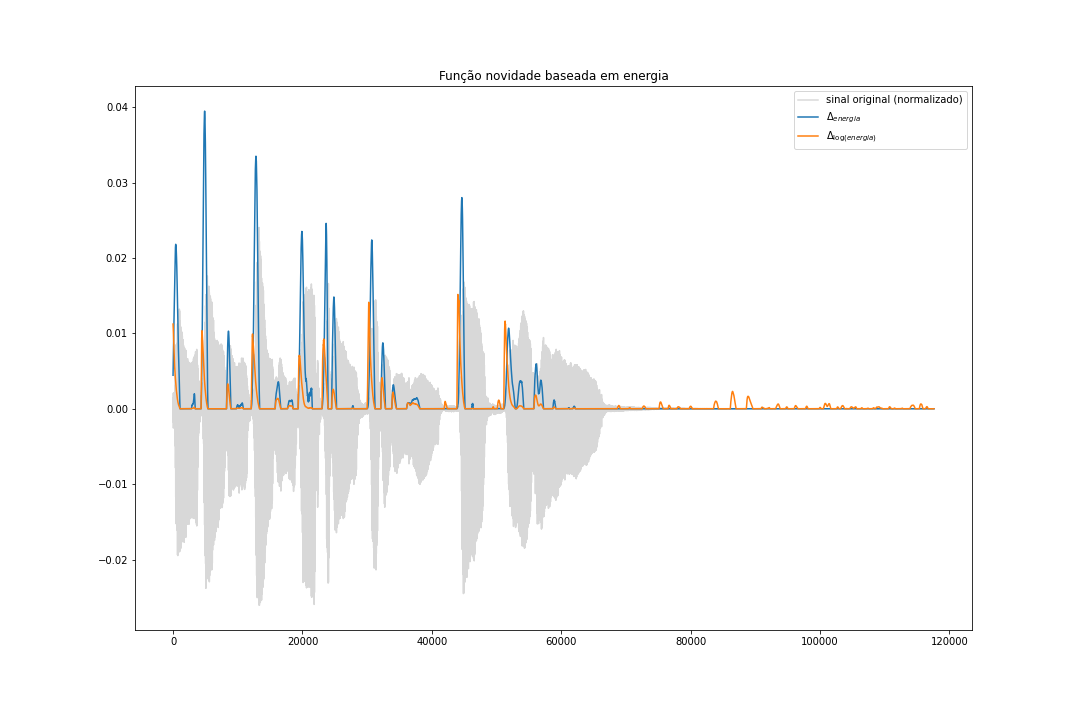
Ao adicionarmos mais instrumentos, a detecção passa a errar a posição dos onsets porque as energias dos sinais se misturam e se somam.
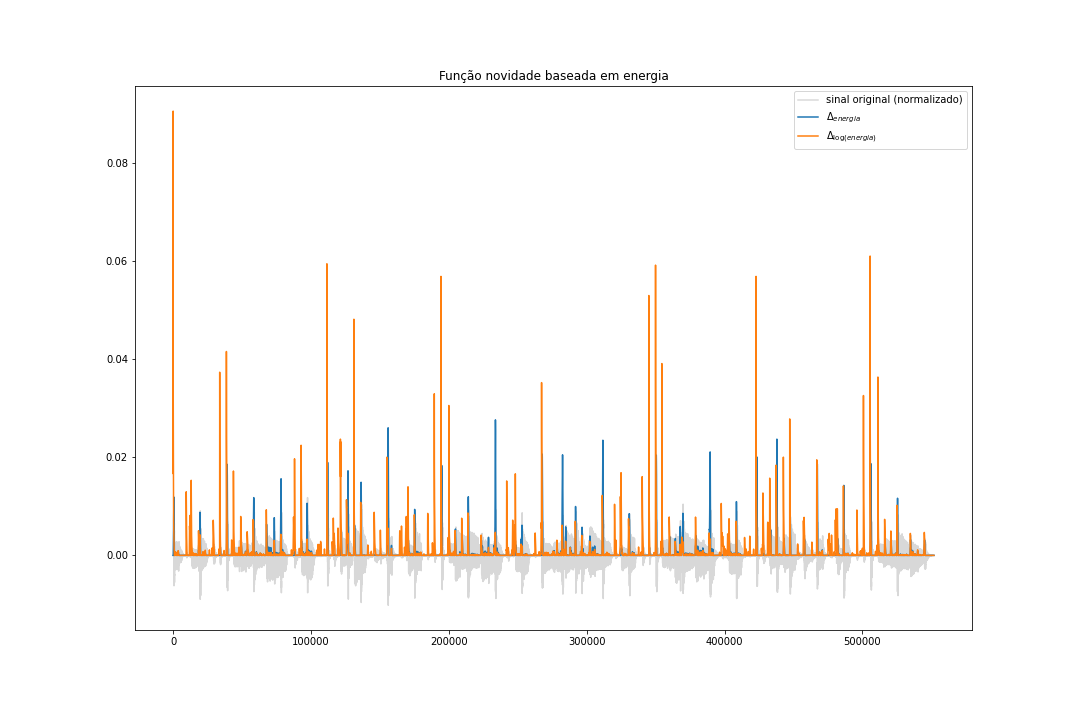
Função novidade baseada em espectro
A função baseada em espectro é baseada no espectro de magnitude do sinal, que, por sua vez, é calculado por meio da Transformada de Fourier. Uma vez que temos o espectro, seguimos quase os mesmos passos da função anterior: primeiro, calculamos as diferenças entre frames seguidos (o chamado fluxo espectral) e aplicamos o retificador de meia onda. Temos os seguintes passos
\[\Delta_{Espectral}(n) = \sum_{k=0}^K \left|\mathcal{Y}(n+1, k) - \mathcal{Y}(n, k)\right|_{\geq 0}\]onde
\[\mathcal{Y} = \log(1 + \gamma \cdot |\mathcal{X}|)\]que representa uma compressão logarítmica.
Existem algumas variações que podem ser feitas a partir do fluxo espectral, considerando outros tipos de distância entre os frames, como, por exemplo, a distância do cosseno, distância logarítmica e etc, mas não vamos entrar nesse detalhe por enquanto.
O primeiro passo é fazer a transformação do sinal do domínio do tempo para o domínio da frequência. Fazemos isso por meio da STFT: $X = STFT(X)$ e então aplicamos a compressão logarítmica, onde buscamos amplificar os espectros menos ruidosos, conseguindo assim detectar os onsets mais fracos, mas que ainda são importantes. Importante lembrar que a amplificação do ruído vai acontecer à medida que $\gamma$ cresce. Essa parametrização deve ser feita de acordo com o problema que estamos tentando resolver.
Abaixo um exemplo da diferença entre alguns parâmetros de $\gamma$ e seus respectivos picos
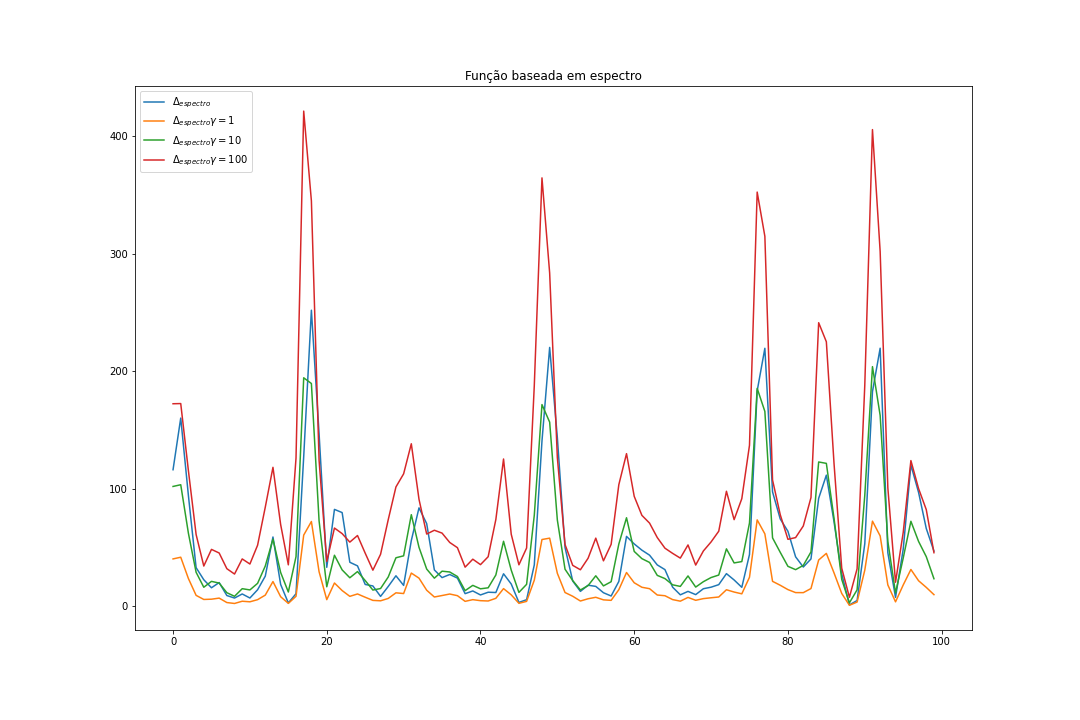
Após a compressão, calculamos a diferença entre os frames subsequentes e aplicamos o retificador de meia onda para descartar as diferenças negativas. Por fim, somamos as diferenças positivas (que, novamente, representam o aumento de energia) para cada um dos bins de frequência, tendo assim a função novidade.
Função novidade baseada em fase
Métodos que se baseiam na fase do sinal assumem que em um momento mais “constante” do sinal há pouca variação de fase. Ou seja, em momentos em que há algum novo acontecimento, como um onset, provavelmente teremos perturbações na fase. O método de cálculo é bastante simples e é feito através do cálculo da segunda derivada da fase, que, de forma intuitiva, mede a taxa de variação da própria variação de uma função. Se dois frames subsequentes têm mais ou menos a mesma taxa de variação então sua diferença será equivalente e a sua derivada de segunda ordem será próxima a zero.
\[\varphi' = \varphi(n) - \varphi(n-1) \\ \varphi'' = \varphi'(n) - \varphi'(n-1)\]E então
\[\Delta_{Fase}(n) = \sum_{k=0}^K |\varphi''(n, k)|\]Aqui, temos dois pontos importantes a serem considerados. O primeiro deles é que a fase na transformada de Fourier é periódica e está restrita ao intervalo de $[0, 2\pi)$ , o que faz que tenhamos “saltos” entre valores uma vez que completamos a volta do círculo unitário. Isso faz com que o cálculo da diferença às vezes resulte valores que estão fora do intervalo desejado.
O problema da função novidade que usa a fase é que quando há pouca variação a fase acaba se tornando muito ruidosa, o que pode fazer com que sejam “adicionados” onsets que na verdade não são nada além de ruído.
Função novidade baseada no domínio complexo
A função baseada no domínio complexo considera tanto o espectro de magnitude do sinal quanto a fase, tendo assim uma abordagem mais robusta para o problema de detecção de onset. Nesse caso, assumimos que tanto a fase quanto a magnitude do sinal é mais ou menos constante em regiões do sinal em que não há muita variação.
A ideia aqui é estimar o que seria o valor do espectro complexo do próximo frame e então comparar a nossa estimativa com o valor real. Se nossa estimativa for muito diferente, ou seja, se houver uma “perturbação” no sinal, provavelmente teremos um onset ou pelo menos um candidato relevante a onset.
A estimativa do espectro complexo é dada por
\[\varphi'(n, k) = \varphi(n, k) - \varphi(n-1, k) \\ \hat{\mathcal{X}}(n+1, k) = |\mathcal{X}(n, k)|e^{2\pi i(\varphi(n, k) + \varphi'(n, k))}\]Assim que temos o valor da estimativa, a função novidade se torna a comparação entre o valor estimado e o valor observado, representando assim o grau de não-estacionariedade daquele frame e daquele coeficiente.
\[\mathcal{X}'(n+1,k) = |\hat{\mathcal{X}}(n+1,k)-\mathcal{X}(n+1,k)|\]Como as outras funções, o resultado dessa diferença não discrimina entre onsets (início da nota ou o aumento de energia) e offsets (fim da nota ou uma diminuição de energia). Pra isso, separamos $\mathcal{X}$ em dois componentes: o de aumento de energia e o diminuição.
\[\begin{eqnarray*} \mathcal{X}^+(n,k) = \left\{ \begin{array}{cl} \mathcal{X}'(n,k) & \, \mbox{for $|\mathcal{X}(n,k)|>|\mathcal{X}(n-1,k)|$}\\ 0 & \, \mbox{caso contrário,} \end{array} \right.\\ \mathcal{X}^-(n,k) = \left\{ \begin{array}{cl} \mathcal{X}'(n,k) & \, \mbox{for $|\mathcal{X}(n,k)|\leq |\mathcal{X}(n-1,k)|$}\\ 0 & \, \mbox{caso contrário.} \end{array} \right. \end{eqnarray*}\]Olhando apenas para as componentes positivas, temos enfim a nossa função novidade ao somarmos os valores por frequência.
\[\Delta_{Complexo} = \sum_{k=0}^K \mathcal{X}^+(n, k)\]Ufa!
Pós-processamento
Todos os métodos citados ainda podem ter etapas de pós-processamento para melhorar a qualidade da função novidade resultante, como por exemplo subtrair a média do sinal -removendo assim pequenas flutuações que podem ser consideradas ruído-, normalizar o sinal e etc.
Detecção de picos
A partir do momento em que a função novidade está calculada, devemos escolher quais os onsets que de fato representam o início de uma nota em vez de um tremolo ou um rubato, por exemplo. Para isso, precisamos fazer a detecção de picos. Se você fechar os olhos por um segundo, é simples de ver: precisamos de encontrar alguns máximos locais e ter certeza de que esses máximos locais estão acima de um valor mínimo para não acabarmos selecionando ruído.
O algoritmo é essencialmente esse! Primeiro, definimos um limiar (threshold) que usaremos como um valor mínimo para um pico ser considerado onset. Esse threshold pode ser fixo (ter o mesmo valor para todo o sinal) ou variável (mudar localmente com o sinal).
Conclusão
Esse foi só uma visão geral dos métodos mais famosos da detecção de onsets. Os parâmetros usados para os métodos variam de problema pra problema: o tamanho da FFT, por exemplo, deve ser menor para aplicações de reconhecimento de fala do que para aplicações em sinais musicais, o $\gamma$ da compressão logarítimica também depende da aplicação para não acabar ressaltando muitos ruídos desnecessários, o cálculo do fluxo espectral pode variar dependendo do problema e etc etc etc. Além disso tudo, nem foi mencionado o processamento em sub-bandas, que é quando dividimos o sinal em bandas de frequência e fazemos a detecção de onsets pra cada uma dessas bandas, de forma a ter um resultado um pouco mais robusto.
Mesmo assim, espero que esse overview tenha sido agradável (na medida do possível, hehehe) e pelo menos um pouco esclarecedor.
Os notebooks com os códigos completos estão neste repositório.
Muito obrigada!
Referências
Bello, Juan Pablo. A Tutorial on Onset Detection
Lecher, Alexander. An Introduction to Audio Content Analysis
Leveau, Methodology and Tools for the Evaluation of Automatic Onset Detection Algorithms in Music
Müller, Meinard. Fundamentals of Music Processing
Wikipédia, Retificador Meia Onda