big data 101
sumário
por que big data?
o gerenciamento de dados evoluiu à medida que a quantidade de dados também evoluiu. no início, tínhamos dados guardados em arquivos e mainframes, evoluímos para bancos de dados relacionais, bancos de dados paralelos, bancos de dados não-relacionais, até que então os bancos de dados não eram mais suficientes pra quantidade massiva de dados disponível.
como nada acontece sozinho, além da evolução de bancos de dados seguiu a evolução de outras áreas da computação, como infraestrutura e hardware (GPUs, por exemplo, foram o que permitiram que o aprendizado de máquina e deep learning existissem da maneira que existem hoje!).
com a nova estrutura e os novos desafios, pesquisas começaram a apontar para big data e como processar esse monte de coisa não estruturada.
MapReduce
o MapReduce foi uma mudança enorme de paradigma para o processo intensivo de dados. se formos falar um pouco de história, o MapReduce foi proposto como um paradigma para resolver o processamento de dados do google!
dentre as ideias e propostas do MapReduce, podemos destacar algumas:
- abstração: separamos o que de como. a programadora especifica as computações que precisam ser feitas e algumas configurações, mas é o runtime que de fato organiza as computações e execuções.
- escala: em vez de ter um computador gigante, temos vários pequenos, que são responsáveis por processar pedaços da entrada. isso é muito mais eficaz!
- tolerância a falhas: por conta da natureza paralela da ideia, o MapReduce é por padrão tolerante a falhas. é um paradigma que espera que falhas vão ocorrer e, por isso, salva os arquivos em pelo menos 3 lugares diferentes no sistema de arquivos e, caso uma tarefa falhe, reinicia automaticamente.
- evitar mover os dados de lugar: em vez de mover os dados, movemos o código, que é muito menor. a computação é feita em nós separados, então faz mais sentido.
- evitar acesso aleatório: o MapReduce foi criado para processamentos em batches e organiza as computações em um grande streaming.
estrutura de um programa MapReduce
- o programa se inicia iterando pelo arquivo.
- mapper: filtra os dados de interesse e os transforma em um par <k,v>. para cada linha do arquivo, o mapper vai enviar um par chave-valor para a próxima fase.
- se todos os mappers terminaram suas execuções, os dados são re-arranjados por chave (tudo que pertence a mesma chave é enviado ao mesmo reducer) e enviados para o reducer. esse passo é conhecido como shuffle.
- reducer: agrega todas as chaves k e seus respectivos valores e então salva os resultados no sistema de arquivos.
pontos importantes:
- no item 1, o sistema de arquivos envia pedaços do arquivo para cada mapper. a ideia é que eles tenham mais ou menos a mesma quantidade para processar e não ter nenhum gargalo de execução (o famoso bottleneck)
- sim, o item 3 pode ser otimizado! vamos falar disso daqui um segundo.
- no item 4, os reducers podem se tornar um gargalo se, por exemplo, uma chave tiver muito mais dados do que todas as outras. isso acontece porque o reducer trabalha direto com a chave. nesse caso, outras técnicas são necessárias.
peguei essa imagem do panorama geral emprestada dos slides da minha aula (talvez no futuro eu a refaça)
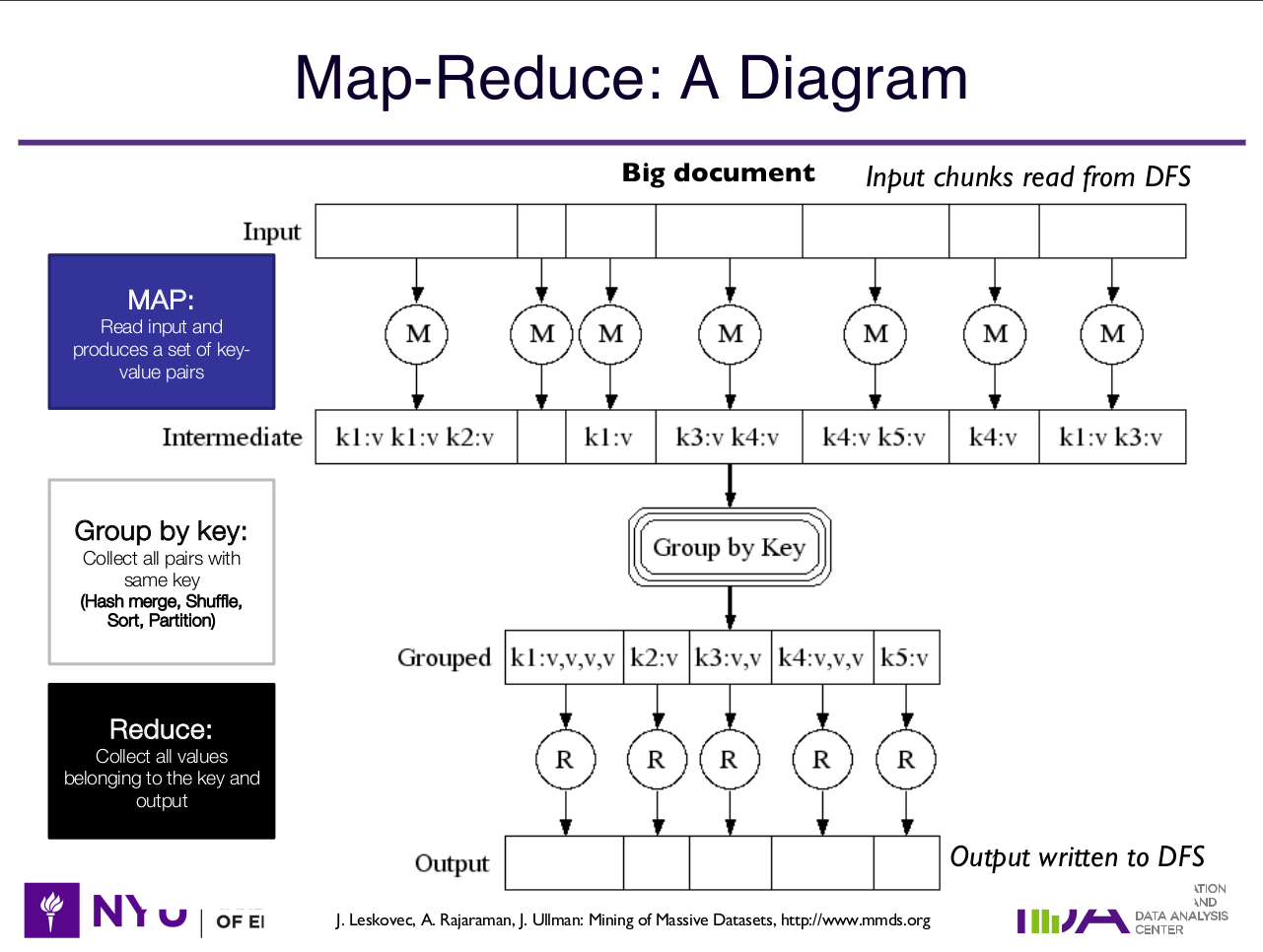
suponha que estamos fazendo um programa que conta palavras da entrada. e o texto para um dado mapper é
eu amo meu gato. meu gato ama comer petisco. eu amo comer pizza.
seguindo a estrutura do programa, o mapper mandaria para o reducer o seguinte
(eu, 1) (amo, 1) (meu, 1) (gato, 1) (meu, 1) (gato, 1) (ama, 1) (comer, 1) (petisco, 1) (eu, 1) (amo, 1) (comer, 1) (pizza, 1)
cada chave é a palavra em si e o valor é “1” porque estamos contando todas elas. teríamos então o agrupamento por chave e o reducer no fim somaria as chaves iguais. no fim, a saída do reducer seria
(eu, 2) (amo, 2) (meu, 2) (gato, 2) (ama, 1) (comer, 2) (petisco, 1) (pizza, 1)
mappers, combiners, partitioners e reducers
os passos de map e reduce são obrigatórios num programa de… MapReduce, mas pra além disso existem mais alguns passos que uma programadora pode ter controle da execução e usar isso para otimizar os seus programas. esses passos são os combiners e partitioners.
no exemplo anterior, mesmo que a mesma palavra apareça mais de uma vez no mesmo mapper, estamos enviando elas separadamente para o reducer. em um texto pequeno isso não é problema, mas quando lidamos com muitos dados isso pode se tornar um gargalo porque no fim das contas uma das operações mais custosas é a de ficar enviando seus dados de um lado pro outro. a comunicação entre programas requer sincronização e a sincronização é uma tarefa custosa.
agora olhamos para os combiners. a ideia dos combiners é ser uma agregação intermediária antes de enviar os dados para o reducer. então no nosso exemplo, o combiner faria a soma das chaves comuns e enviaria para o reducer os resultados já agregados daquele mapper. dessa forma, o reducer tem apenas a missão de agregar as chaves comuns de diferentes mappers!
aqui mais um slide roubado que talvez eu refaça a imagem no futuro:
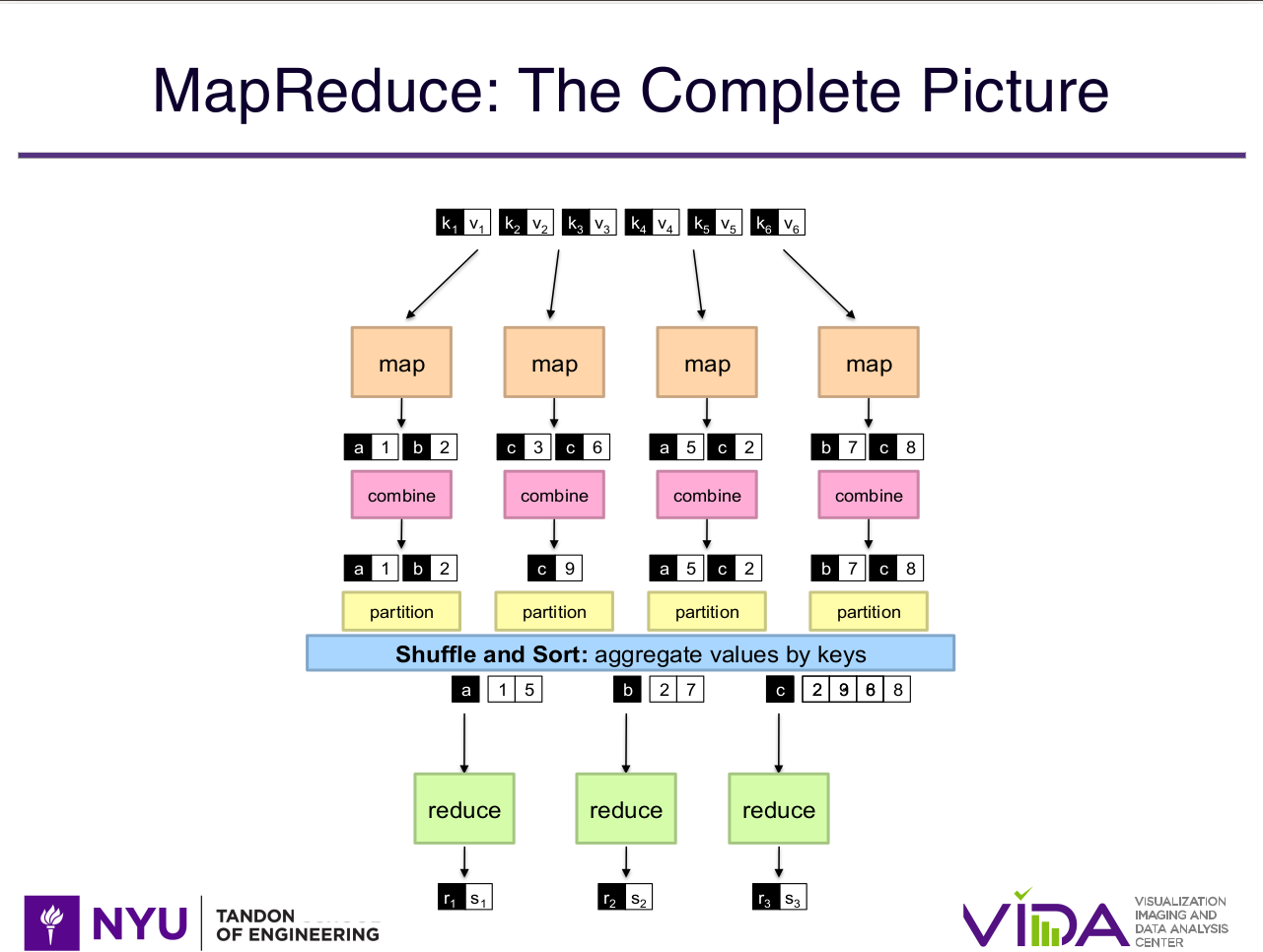
existem duas formas de se utilizar o combiner:
- você de fato implementa um combiner. esse caso geralmente é mais custoso porque tem escrita e leitura de disco associada, mas funciona e é o indicado quando você tem uma redução mais complexa.
- in-mapper combiner: nesse caso, você faz a combinação dentro do próprio
mapper. a maior vantagem é a velocidade, porque você está processando tudo em
memória e enviando os resultados já agregados daquele mapper. se os seus dados
agregados não couberem em memória, essa técnica não vai funcionar e seu
programa será provavelmente interrompido, então avalie com cuidado!
- é possível gerenciar a memória do in-mapper combiner, mas isso é mais um ponto de complexidade que você está adicionando ao seu fluxo.
MapReduce e bancos de dados paralelos
antes do MapReduce surgir, os bancos de dados paralelos já existiam. não é de se espantar que a turma do banco de dados não gostou nem um pouco do MapReduce e na verdade eles publicaram um artigo levemente mal-educado comparando as duas abordagens, dizendo que o MapReduce não era uma ideia nova, que não era performático e que tudo que os autores estavam tentando fazer já era feito por banco de dados paralelos.
fofocas à parte, qual a diferença entre as duas abordagens?
os bancos de dados paralelos requerem uma estrutura um pouco maior e melhor do que o MapReduce e por isso são mais caros.
em contrapartida, os bancos de dados paralelos são muito mais rápidos para tarefas simples, enquanto o MapReduce tem um overhead muito grande, ou seja, não faz sentido inicializar uma estrutura enorme para fazer uma simples query. pra além disso, uma grande vantagem é você ter o SQL para manipular esses dados e não ter que ficar se preocupando em como as coisas funcionam debaixo dos panos: tanto faz qual o lugar em que o dado está salvo, se é paralelo ou não, qual o tamanho do cluster e etc. isso tudo é problema do DBA, você só precisa escrever sua query!
no geral, MapReduce é mais útil para tarefas mais complexas e por isso você precisa ter a mesma flexibilidade de uma linguagem de programação. é indicado para dados não-estruturados e processamentos intensivos.
a coisa mais importante que eu quero pontuar aqui é que o MapReduce e os bancos de dados paralelos são feitos para tarefas distintas. não é como se um quisesse substituir o outro. são casos de uso diferentes.
uma opção para ter o melhor dos dois mundos é definir um esquema e salvar os resultados do seu MapReduce em um banco de dados, de forma que análises e queries mais simples e repetitivas possam ser performadas de maneira eficiente.
MapReduce e Spark
como discutido na seção anterior, o nosso colega MapReduce (MR) é ótimo pra grandes trabalhos em batch, mas não faz sentido para programas pequenos e rápidos. por causa disso, não é eficiente para análises interativas, queries e aplicações em vários estágios. você precisaria encadear uma série de mappers e reducers para conseguir isso e precisaria escrever todos os resultados intermediários em disco. além disso, MR é extremamente baixo nível e você tem que implementar todas as operações necessárias: filtros, joins, agregações etc.
foi nesse contexto que o Spark foi criado. a principal ideia é conseguir usar a memória principal (e não a escrita em disco) pra compartilhar dados entre estágios de processamento, e criar um framework com operações básicas que facilitem a vida de quem está programando.
o RDD (Resilient Distributed Dataset) é a base do Spark e uma estrutura imutável de dados que você consegue manter em memória e aplicar transformações (filtro, join, groupby etc). como é imutável, cada transformação cria um novo RDD, o que permite que você consiga “voltar atrás” caso haja falhas no sistema e recuperar o que foi feito em passos anteriores.
outro ponto importante do Spark é o lazy evaluation: existem funções que são apenas transformações e existem funções que são ações. transformações são todas empilhadas até que uma ação seja feita. quando uma ação é feita, o runtime checa qual a melhor ordem de executar as transformações e então as executa.
o Spark é 10 e tem APIs pra várias linguagens de programação diferentes, como Scala (sua linguagem principal), Python (o famoso PySpark), Java e R. em comparação com o MR, o Spark é até 100x mais rápido em memória e 10x mais rápido em disco.
regras de associação
regras de associação são uma técnica de mineração de dados pra que a gente consiga encontrar padrões, relações e modelos nos dados que nos tragam informações inesperadas e úteis.
o que nós queremos aqui é achar uma regra do tipo $I \rightarrow j$, que significa “se \(I\) for comprado, \(j\) vai ser comprado também”.
o exemplo mais famoso disso foi a relação encontrada entre compras de fraldas e cerveja, que motivou alguns supermercados a deixar os itens próximos. embora num primeiro momento fosse estranho notar nos dados que essas coisas fossem compradas juntas, logo perceberam que a motivação por trás é que papais e mamães que estão ali no mercado comprando fraldas não vão ter tempo pra sair e se divertir, então a diversão talvez fique em casa mesmo.
itens frequentes
definições e fórmulas:
- suporte: contagem dos itens I
- item frequente: tem o suporte maior que o suporte mínimo
- confiança: determina o quão certa você está de que aqueles dois produtos serão
“comprados” juntos.
- \[conf(I \rightarrow j) = \frac{sup(I \cup j)}{sup(I)}\]
- interesse: nem toda confiança alta é interessante. se I = “leite” e j =
“café”, essa regra não nos diz nada de útil. por isso, temos uma medida
específica de interesse:
- \[interest(I \rightarrow j) = conf(I \rightarrow j) - P(j)\]
- lift: é um tipo de medida de correlação
- \[lift(I \rightarrow j) = \frac{P(I \cup j)}{P(I)P(j)}\]
a imagem abaixo mostra e define os itens frequentes, itens fechados e itens
maximais:
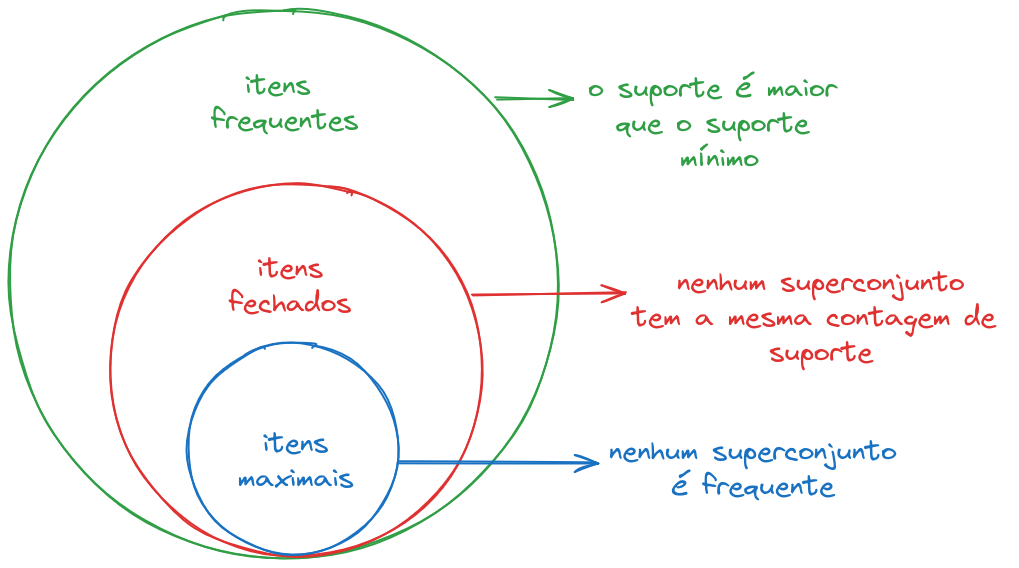
esses conjuntos de itens frequentes tem uma propriedade importante chamada monotonicidade.
se I é um conjunto frequente, então subconjuntos de I também são.
essa propridade nos permite comprimir a representação de um conjunto frequente, por exemplo, usando o conjunto maximal. se um conjunto é maximal, então todos os seus subconjuntos são frequentes.
algoritmo a priori
a monotonicidade nos permite implementar um algoritmo interessante para encontrar itens frequentes: o algoritmo a priori.
a primeira passada do algoritmo filtra todos os itens não frequentes. na segunda passada, serão analisados somente os itens frequentes e seus superconjuntos. se seu super conjunto também for frequente, ele se mantém.
o problema desse algoritmo é que se você quer um conjunto de tamanho N, você precisa fazer N passadas pelos dados e isso pode ser muito custoso. uma forma de reduzir o custo é usando um sampleamento aleatório, e fazendo o a-priori dentro desse subconjunto. ou seja
- lê subconjuntos aleatórios que são uma fração p dos dados
- determina quais são os itens frequentes (ou seja, maiores que o suporte s*p)
- salva os itens frequentes de todos os subconjuntos
- faz uma união dos resultados e verifica quais são maiores que o suporte s
similaridade
encontrar documentos similares é uma tarefa importante por vários motivos, porém não é algo trivial porque existem vários pontos de vista diferentes.
a técnica para encontrar documentos similares antes precisa definir se é necessário encontrar documentos um pouco similares ou muito similares. o caso de documentos muito similares é mais simples, então vou descrever brevemente as técnicas apenas para os pouco similares. é também importante pontuar que estamos vendo similaridade de documentos a nível de palavras, mas não estamos levando em consideração contexto ou semântica!
similaridade de Jaccard
a similaridade de Jaccard é um método pra conseguir mensurar a similaridade entre dois conjuntos. ela é definida por
\[J(A, B) = \frac{A \cap B}{A \cup B}\]porque essa similaridade é feita entre conjuntos, ela não leva em consideração a quantidade de vezes que uma palavra aparece, mas apenas se ela aparece ou não.
importante: no caso dos vetores binários, intersecção = “e” lógico e união = “ou” lógico. ou seja, a gente tem que lembrar das tabelas verdades (tabela-verdades? tabelas-verdades? tabelas-verdade? enfim, você entendeu).
“ou”
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
“e”
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
exemplo
considerando os vetores A = 1111000000 e B = 0100100101 e C = 0000011110, temos
\[J(A,B) = \frac{A \cap B}{A \cup B} = \frac{1}{7}\] \[J(A,C) = \frac{A \cap C}{A \cup C} = \frac{0}{8} = 0\] \[J(B,C) = \frac{B \cap C}{B \cup C} = \frac{1}{7}\]finalmente, a distância de Jaccard é dada por
\(d(x,y) = 1 - s_J(x,y)\).
no caso dos exemplos acima, temos
\[d(A,B) = 1 - J(A,B) = 1 - \frac{1}{7} = \frac{6}{7}\] \[d(A,C) = 1 - J(A,C) = 1\] \[d(B,C) = 1 - J(B,C) = \frac{6}{7}\]similaridade do cosseno
\[\cos(p_1, p_2) = \frac{p_1\cdot p_2}{||p_1||_1 \cdot ||p_2||_2}\]exemplo
dados os vetores u = [1, 0.24, 0, 0, 0.5, 0]$, v = [0.75, 0, 0, 0.2, 0.4, 0] e w = [0, 0.1, 0.75, 0, 1], temos as seguintes similaridades
\[\begin{align*} \cos(u,v) &= \frac{1\times 0.75 + 0.5\times0.4}{\sqrt{1^2 + 0.25^2 + 0.5^2}\sqrt{0.75^2+0.2^2+0.4^2}} \\ &= 0.9496 \end{align*}\]e seguindo a mesma fórmula, \(\cos(v, w) = 0\), \(\cos(u,w) = 0.01740\) e \(\cos(v,w) = 0\).
consideramos agora os vetores binários A, B e C do exemplo anterior.
\[\cos(A,B) = \frac{1}{\sqrt{4}\sqrt{4}} = \frac{1}{4}\] \[\cos(A,C) = \frac{0}{\sqrt{4}\sqrt{4}} = 0\] \[\cos(B,C) = \frac{0}{\sqrt{4}\sqrt{4}} = 0\]aqui, igual a distância de Jaccard, temos que \(d(x,y) = 1 - \cos(x,y)\).
distância de edição
métrica para comparar a distância entre strings. é também conhecida como distância de Levenshtein. a ideia é mensurar quantas remoções e quantas adições são necessárias para converter uma string em outra.
por exemplo, queremos converter ele -> além
- remove
e(le) - insere
a(ale) - insere
m(alem)
a distância então é 3.
uma forma mais direta de fazer essa medida é olhando para a LCS (longest common subsequence), ou subsequência comum mais longa. a LCS é a maior subsequência que os dois termos têm em comum. a fórmula então se torna
\[d(x,y) = |x| + |y| - 2|LCS(x,y)|\]exemplo
no nosso exemplo, temos |x| = |ele| = 3, |y| = |além| = 4 e LCS(x,y) = |le| = 2,
uma vez que a maior subsequência é le. substituindo, temos
shingling
a técnica de *shingling” (ou n-gramas) é uma forma de dividir textos ou palavras em subconjuntos de tamanho “n”. a partir disso, podemos calcular a similaridade entre os dois conjuntos.
usemos de exemplo a frase
“big data e data big”
assumindo shingles de 3 caracteres e a remoção dos espaços, temos os shingles
{“big”, “igd”, “gda”, “dat”, “ata”, “tae”, “eda”, “dat”, “ata”, “tab”, “abi”, “big”}
removendo as repetições
{“big”, “igd”, “gda”, “dat”, “ata”, “tae”, “eda”, “tab”, “abi”}
o shingle também pode ser, por exemplo, 2 palavras:
{“big data”, “data e”, “e data”, “data big”}
e assim por diante. a vantagem de existir essa sobreposição de um termo é que você mantém a estrutura do seu documento. escolher o tamanho do shingle depende da tarefa que a gente tá querendo resolver e eu não vou entrar em detalhes.
min-hashing
o minhashing é uma função pra reduzir o tamanho de uma representação. a ideia é que a gente sempre pegue o valor mínimo de uma matriz de assinaturas (na prática, é uma representação mais esparsa usada)
por exemplo, suponha que temos a seguinte tabela:
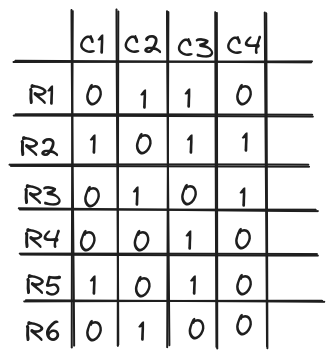
cada columa representa uma assinatura diferente. o primeiro passo é permutar as linhas, como na imagem abaixo

depois da permutação, calculamos o menor valorpara cada uma das colunas C e então esse é o nosso resultado da função minhash. no caso de vetores binários, como o do nosso exemplo, calculamos o primeiro valor diferente de 0. então temos o seguinte resultado para essa permutação:
- minhash(C1) = R5
- minhash(C2) = R6
- minhash(C3) = R4
- minhash(C4) = R3
na prática a permutação não é usada porque ela é muito custosa. em vez disso, usam-se diferentes funções de hashing e então calcula-se o menor valor. abaixo um exemplo:
LSH (Locality Sensitivity Hashing)
como já disse algumas vezes, na prática é muito custoso a gente calcular pares que são similares porque estamos o tempo todo comparando vetores muito longos. para aproximar e diminuir a complexidade desse cálculo, usamos várias aproximações. a figura abaixo mostra um exemplo dos passos que temos que passar até de fato conseguirmos pares de documentos que são similares.
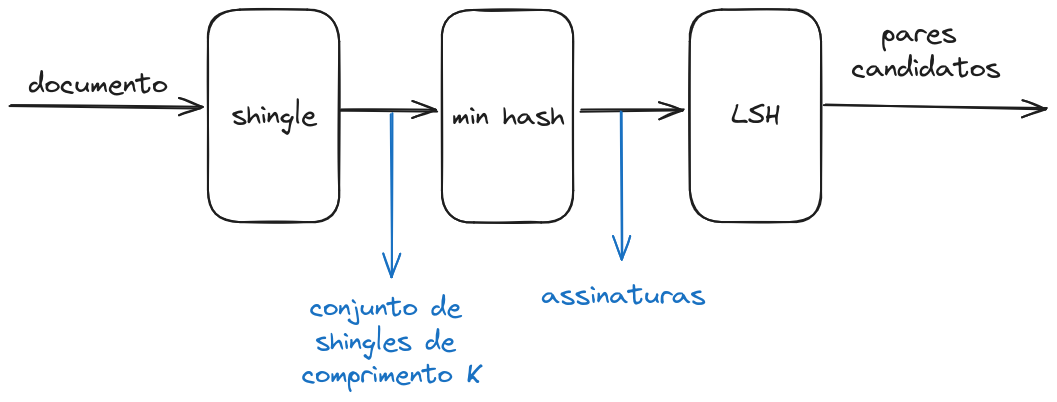
a ideia do LSH é você dividir a sua matriz de assinaturas em bandas e então comparar o quão similares suas linhas são dentro de cada banda. se você tem um par candidato, então a similaridade desse par pode enfim ser avaliada. por exemplo, se temos uma matriz com 10 linhas, podemos ter as seguintes configurações de bandas:
- 1 banda de 10 linhas
- 2 bandas de 5 linhas
- 5 bandas de 2 linhas
- 10 bandas de 1 linha
a primeira e segunda configurações tem algumas propriedades interessantes. quando você tem apenas uma banda, não há nenhuma chance de você ter um falso positivo, ou seja, pares de candidatos que na verdade não são semelhantes. isso acontece porque você está comparando todas as posições da assinatura do documento.
já no caso de se ter 10 bandas, você tem 100% de chance de ter um falso positivo. isso se deve ao fato de você estar comparando apenas uma posição da assinatura do documento então qualquer combinação positiva marcará aqueles dois documentos como similares, o que não necessariamente é verdade.
referências
- Closed Frequent Itemset - The Data Mining Hypertextbook
- Explicando o algoritmo de Regra de Associação - Diego Nogare
- Mining of Massive Datasets
- Slides da Prof. Dr. Juliana Freire
- Spark RDD Programming Guide
bom, essa postagem é mais pra mim do que pra qualquer outra pessoa, mas se tudo der certo, outro alguém também conseguirá aproveitar esse conteúdo. quaisquer erros, me avisa por email.
tchau!